-
Jonas KOKO : Associate Professor in Applied Mathematics
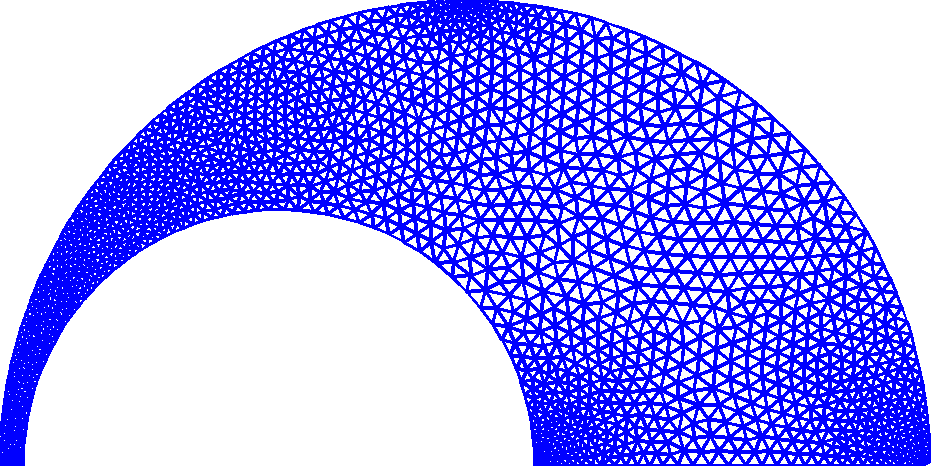
KMG2D : 2D Mesh Generator using signed distance function and a geometric mesh size function
|
Ω={x | φ(x)<0}
where φ is a real-valued function defined on R2.
The code generates unstructured (linear or quadratic) triangular
mesh. The mesh size is automatically adapted to the "thickness"
of the computational domain, using a geometric mesh size
function based on distance from the medial axis. The
medial axis is the set of interior points that have equal
distance to two or more points on the boundary. Computing the
medial axis of a domain requires solving of the eikonal equation||∇ φ(x)|| = 1.
To save computational time, the code uses an approximate
medial axis set. The code can also use a user supplied mesh size
function.The names of the functions and their purposes:
Package: kmg2d Reference : J. Koko, A MATLAB mesh generator for the two-dimensional finite element method, Applied Mathematics and Computation 250, 650-664 (2015). |
 |

|
 |
|
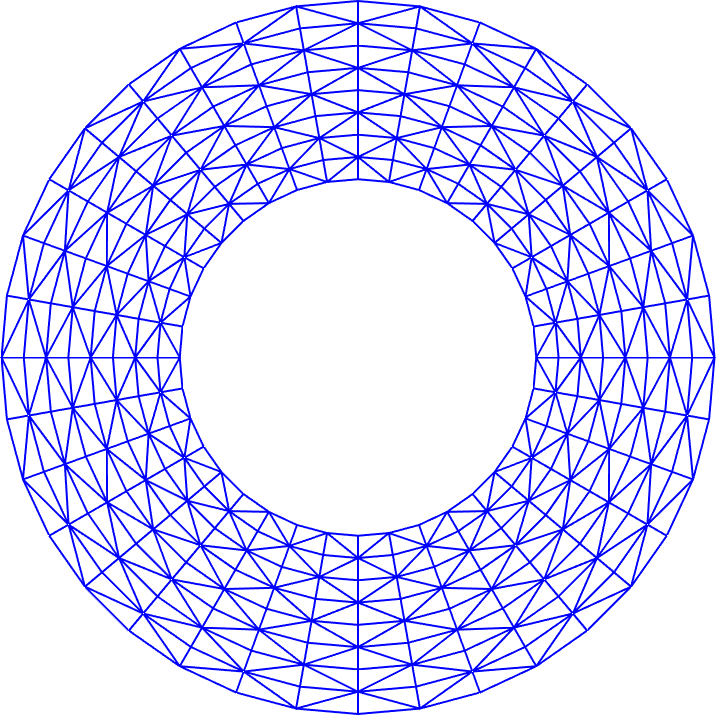
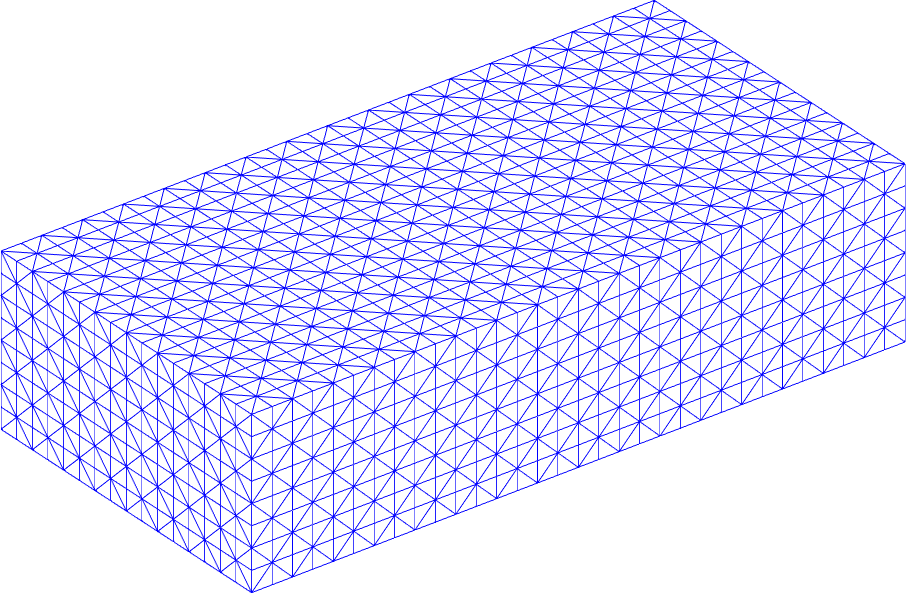
Uniform mesh generation for domains with simple geometry (New)
Two-dimensional domain: kmg2du.m
 |

|
 |

|
Three-dimensional domain: kmg3du.m
 |

|
 |

|
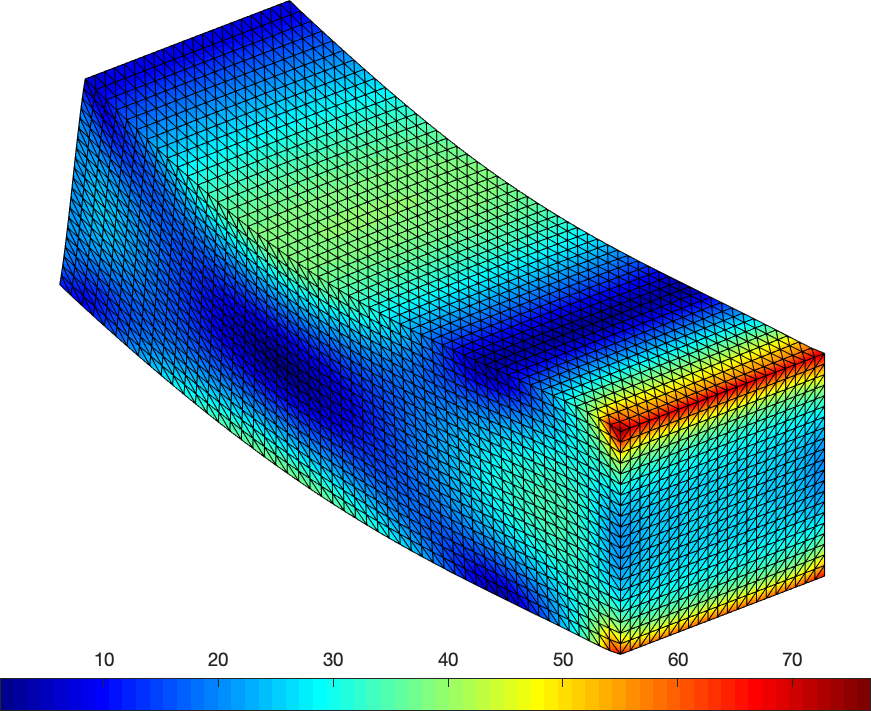
KPDE : Fast FEM assembling functions for the Poisson problem and the linear elasticity in 2D/3D
kpde is
a vectorized MATLAB/OCTAVE library of P1 finite
element assembling functions for the numerical solution of the
Poisson problem and the linear elasticity problem in 2D/3D.
Cell-arrays are used to store the gradient of the element basis
functions. The resulting vectorized MATLAB implementation, close
to the standard form, is fast and scalable. The code consists of
3 sets of functions
Package: kpde Reference: J. Koko, Fast MATLAB assembly of FEM matrices in 2D and 3D using cell-array approach, International Journal of Modeling, Simulation and Scientific Computing 7 (2), 1650010, 2016, DOI: 10.1142/S1793962316500100. |
 |
|
KSTOK : Fast assembling functions for the Stokes equation with mini-element (P1-bubble/P1) in 2D/3D.
kstok
is a vectorized MATLAB assembling functions for the numerical
approximation of the Stokes problem using P1-bubble/P1
finite element in 2D and 3D. The implementation uses
cell-array to store the gradient of the element basis functions.
Consequently, the current code is about two times faster than
the previous one (see below). Note that, the code shares some
functions with kpde
package. The code consists of 3 sets of functions
Package: kstok Reference: J. Koko, Efficient MATLAB codes for the 2D/3D Stokes equation with the mini-element , Informatica 30 (2), 243-268, 2019. |
 |

|
|


